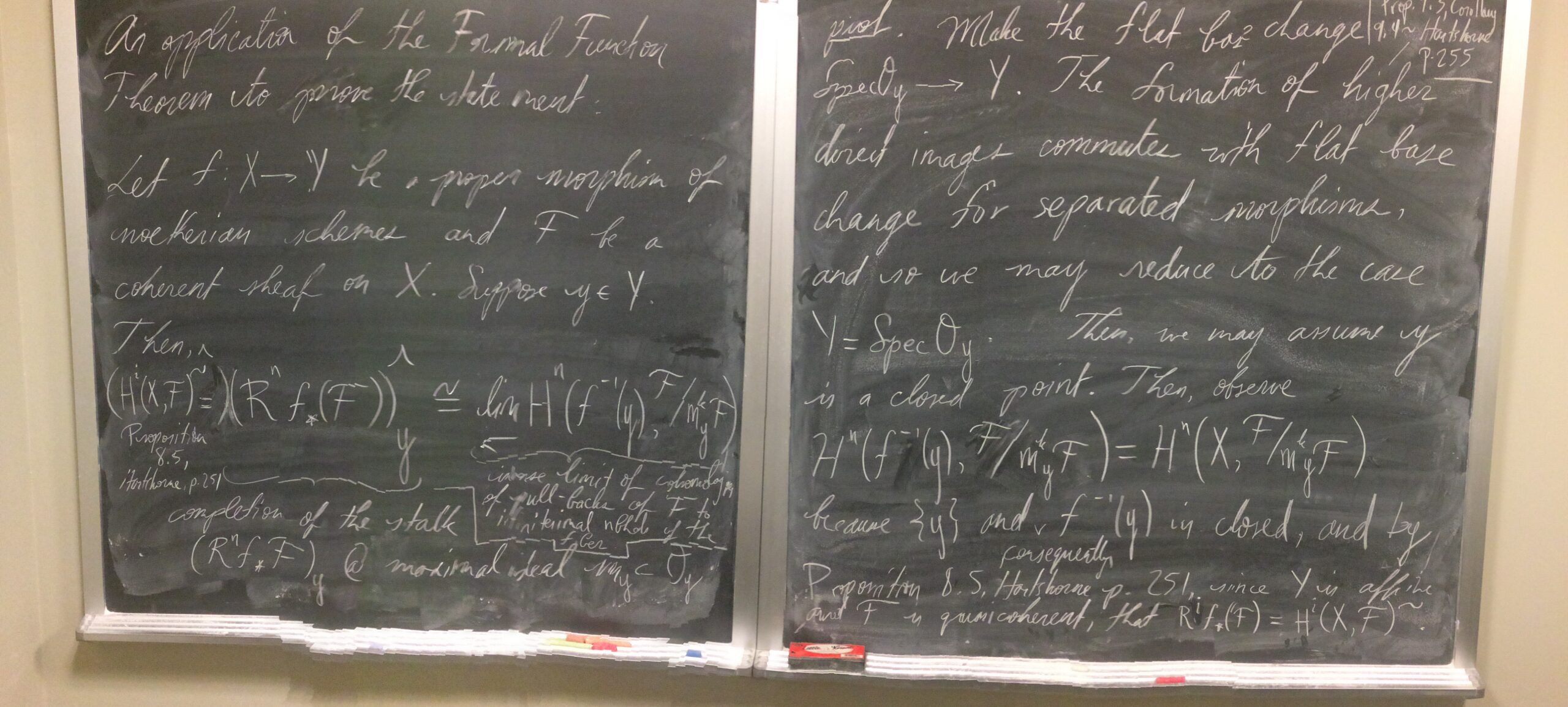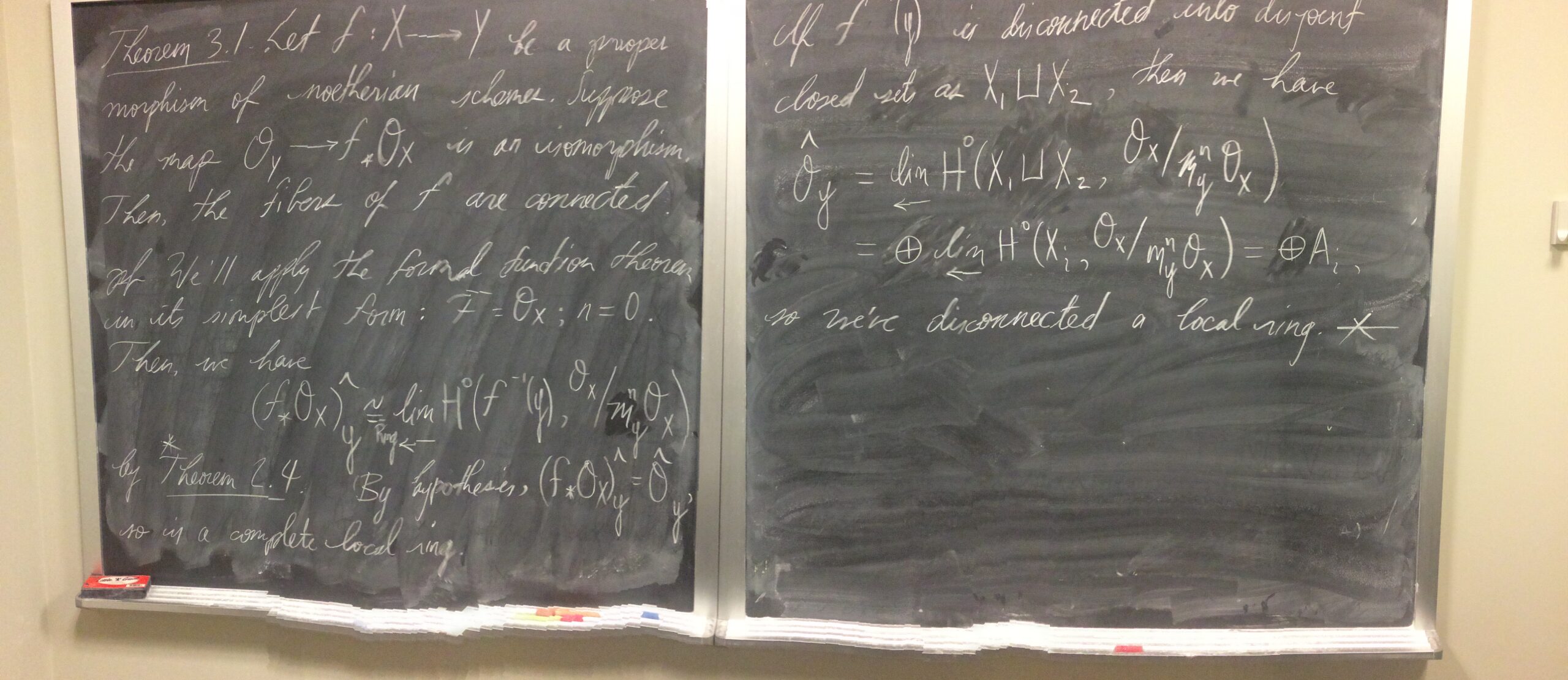- Here is a poster created for Fall 2024 Algebraic Geometry Northeastern Series (AGNES) summarizing progress toward my thesis project to explicitly produce a regular model of a hyperelliptic curve in “bad” (mixed) characteristic (0, 2): poster for Fall 2024 AGNES
- Here are slides from a talk relating mathematics & music (featuring an award-winning app/game I designed, and which Kyle McGrath brought to further fruition) for the 2024 Math League International Summer Tournament at The College of New Jersey: slides from mathemusical talk
- Here are slides from a “lightning talk” given at The Mordell Conjecture 100 Years Later conference at Massachusetts Institute of Technology (MIT) regarding an exemplary construction of a regular model of a (hyper)elliptic curve via normalization of an Obus-Srinivasan model of the projective line some of whose points’ regularity is confirmed via a criterion I’ve established (to appear in my thesis): slides from lightning talk at “The Mordell Conjecture 100 Years Later”
- Here are slides from a talk given at the 2024 CTNT (at the University of Connecticut (UConn)) regarding further progress toward my thesis project advised by Andrew Obus. The focus is (still) on a (fairly) recently (at the time of the talk) established criterion to verify the regularity of the normalization of a curated “Obus-Srinivasan” model of the projective line, but delves a bit further into the “mechanics” of what’s called an Obus-Srinivasan model: slides from talk at 2024 CTNT
- Here are slides from a talk given at the 49th Annual New York State Regional Graduate Mathematics Conference regarding progress toward my thesis project advised by Andrew Obus. The focus is on a recently (at the time of the talk) established criterion to verify the regularity of the normalization of a curated “Obus-Srinivasan” model of the projective line: slides from 49th Annual New York State Regional Graduate Mathematics Conference
- Here are slides from a (short) talk given at the Spring 2024 Algebraic Geometry Northeastern Series (AGNES) regarding further progress Raymond van Bommel, Michael Montoro had made toward the establishment of a new algorithm to resolve the singularities of a curve defined over a field of positive characteristic, adapted from a recent algorithm of Dan Abramovich, Michael Temkin, and Jaroslaw Wlodarcyzk (and independently, Gianluca Marzo and Michael McQuillan) to resolve the singularities of any variety defined over a field of characteristic 0: slides from Spring 2024 AGNES
- Here are slides from a talk I gave at the 2024 Joint Mathematics Meetings regarding the progress Raymond van Bommel, Michael Montoro had made toward the establishment of a new algorithm to resolve the singularities of a curve defined over a field of positive characteristic, adapted from a recent algorithm of Dan Abramovich, Michael Temkin, and Jaroslaw Wlodarcyzk (and independently, Gianluca Marzo and Michael McQuillan) to resolve the singularities of any variety defined over a field of characteristic 0: slides from 2024 JMM
- Here is a link to a Google Drive folder containing handwritten notes I’ve taken for Aise Johan de Jong’s Spring 2021 University of Washington course on alterations: notes for Johan de Jong’s course on alterations
- Here is a link to a site directing to Google Drive folders containing handwritten notes I’ve taken for Dennis Sullivan’s Fall 2020 and Spring 2021 Topology courses: notes for Dennis Sullivan’s Fall 2020 course
- Here is a link to “the chalkboard” from a talk I gave about Serre’s Tor formula following closely Appendix A of Robin Hartshorne’s Algebraic Geometry and an exercise from David Eisenbud’s Commutative Algebra with a View Toward Algebraic Geometry : “chalkboard” from talk
- Here is a link to “the chalkboard” from a talk I gave about stacks as categories fibered in groupoids with an emphasis on the moduli stack of curves following closely Jarod Alper’s Spring 2021 “Introduction to stacks and moduli” and with an eye on Aise Johan de Jong’s paper Smoothness, Semistability, and Alterations, which uses related ideas:“chalkboard” from talk about categories fibered in groupoids
- I became fascinated one semester with the inner workings of Macaulay2, and so investigated the underlying algorithm within that computes the integral closure. Here is a link to some notes I prepared for a talk exposing the algorithm, following closely Theo de Jong’s article regarding this: investigation of algorithm to compute integral closure
- Here is a link to some notes I wrote to prepare a talk about the Riemann-Hurwitz theorem and the sheaf of differentials closely following the discussions from Chapter 16 of David Eisenbud’s Commutative Algebra with a View Toward Algebraic Geometry and Chapter II.8 of Robin Hartshorne’s Algebraic Geomtry. I imagine very little of this is new to anyone, but it might be nice to read for someone just learning it: notes from talk on Riemann-Hurwitz & sheaf of differentials
- Here is a link to some notes I wrote to prepare a talk about the Nullstellensatz following closely David Eisenbud’s discussion in Chapter 4 of Commutative Algebra with a View Toward Algebraic Geometry. Again, I imagine very little of this is new to anyone, but it might be nice to read for someone just learning it: notes from talk on Nullstellensatz à la Eisenbud (& Jacobson)
-
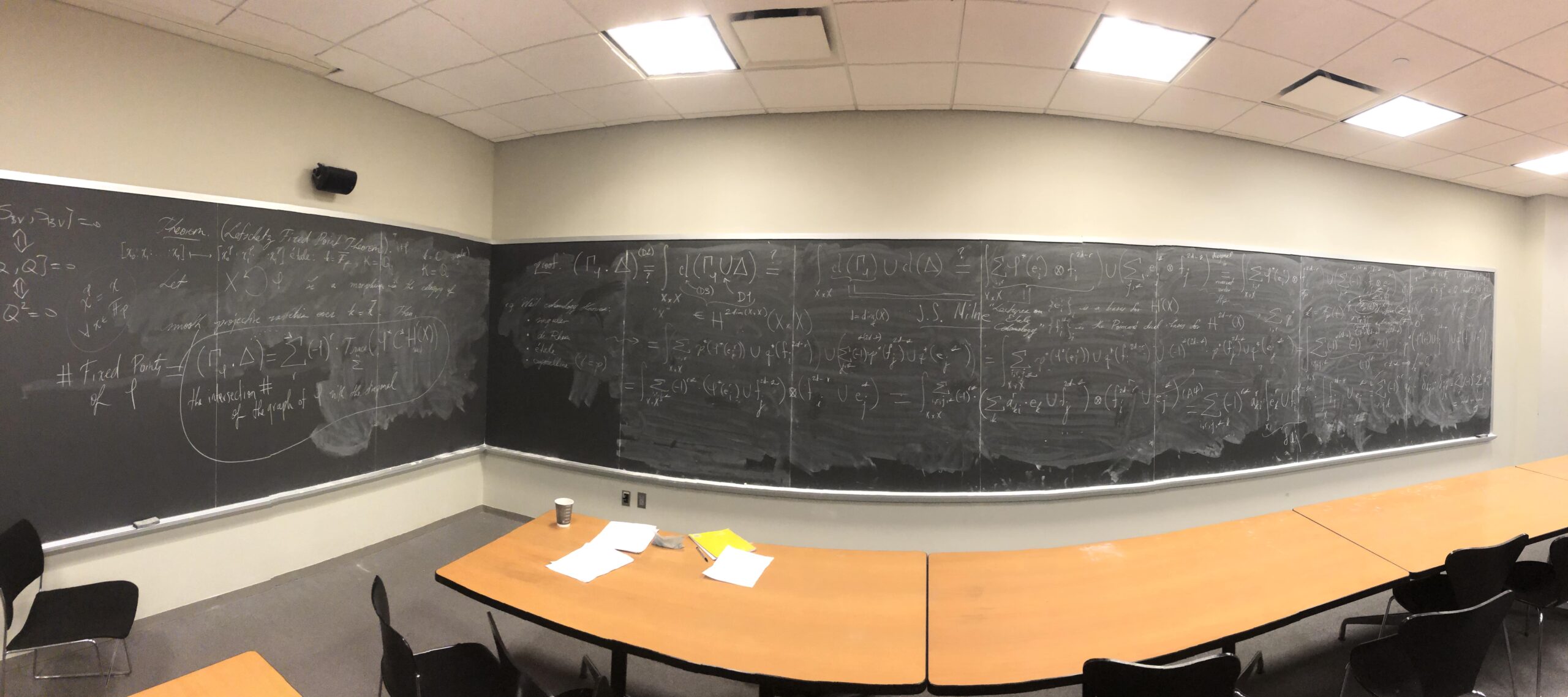
Chalkboard from talk on the Grothendieck-Lefschetz trace formula for an arbitrary Weil cohomology theory
-
This is boardwork for preparation for a talk I gave in Fall 2018 on Zariski’s Main Theorem
further boardwork for the talk on Zariski’s Main Theorem
further boardwork for the talk on Zariski’s Main Theorem
further boardwork for the talk on Zariski’s Main Theorem
further boardwork for the talk on Zariski’s Main Theorem
This entry is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International license.
